K-Map
A Karnaugh map (K-map) is a visual method used to simplify the algebraic expressions in Boolean functions without having to resort to complex theorems or equation manipulations. A K-map can be thought of as a special version of a truth table that makes it easier to map out parameter values and arrive at a simplified Boolean expression.
A K-map is best suited for Functions with two to four variables. Although K-maps can be used for functions with five or six variables, the process is more difficult.
Solving an Expression Using K-Map
Here are the steps that are used to solve an expression using the K-map method:
- Select a K-map according to the total number of variables.
- Identify maxterms or minterms as given in the problem.
- For SOP, put the 1’s in the blocks of the K-map with respect to the minterms and put 0’s at all other cells of K-map.
- For POS, put 0’s in the blocks of the K-map with respect to the maxterms and put 1’s at all other cells of K-map.
- Make rectangular groups that contain the total terms in the power of two, such as 2,4,8 ..(except 1) and try to cover as many numbers of elements as we can in a single group.
- From the groups that have been created in step 5, find the product terms and then sum them up for the SOP form.
Example 1:
The following function defines a basic Boolean expression that incorporates the function’s four variables:
f(A, B, C, D) = A̅BC̅D + ABC̅D̅ + ABC̅D + ABCD + ABCD̅ + AB̅CD + AB̅CD̅
= 0101 + 1100 + 1101 + 1111 + 1110 + 1011 + 1010
= ∑ (5, 12, 13, 15, 14, 11, 10)
= ∑ (5, 10, 11, 12, 13, 14,15)
As per step-1, we need to take 4-variable K-map to solve above expresssion
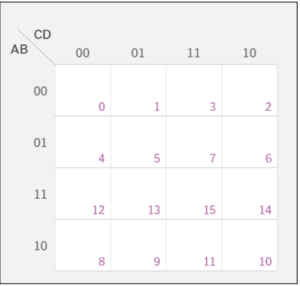
Since we have already found out the minterms ∑ (5, 10, 11, 12, 13, 14,15)
As per step-3, let’s put the 1 at the place of minterms and put 0 at remaining cells of the K-map as shown below
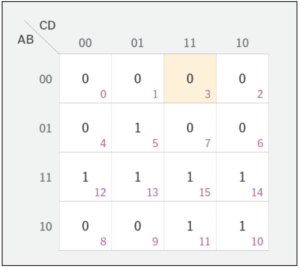
After we’ve set up the K-map, we can start grouping the 1s together to come up with an equation for each group.
We can create groups only horizontally and vertically as shown below by accommodating maximum 1’s in a group.
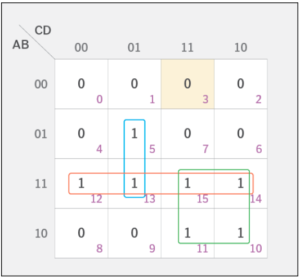
In the case of the expression shown above, there are three groups that meet the criteria, as indicated here.
The red group includes all cells in the third row (12, 13, 15 and 14),
the green group includes four cells from the third and fourth rows (15, 14, 11 and 10)
the blue group includes cells 5 and 13.
Each 1 cell needs to be accounted for, even if it means overlapping. For example, the red group overlaps with the blue and green groups.
After you identify the groups, you can start to calculate your final expression. For each group, determine which parameters do not change, using the row and column binary labels and take them in final expression.
For example, In Green Group, from rows we can see 11(AB) & 10(AB̅) and we should choose parameters that do not change, so take A from rows
From columns we can see 11(CD) & 10(CD̅) and we should choose parameters that do not change, so take C from columns
So the final result for the Green group is AC.
Similarly, the red group can be represented as AB. and Blue group can represented as BC̅D
Which results in final simplified expression is as given below
f(A, B, C, D) = AB + AC + BC̅D
Example 2 :
F (A, B, C, D) = ∑(0, 2, 5, 7, 8, 10, 13, 15)
From the red group, the product term would be BD
From the purple group, the product term would be B̅D̅
If we sum these product terms, then we will get this final expression
F (A, B, C, D) = BD + B̅D̅